To describe y^e Parabola (& other figures
after y^e same manner) pretty exactly.

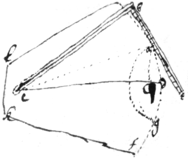
Thake a squire $\mathrm{cbe}$, soe y^t $\mathrm{cb}=\frac{\mathrm{r}}{2}$
(for then the [illeg] circle described by $\left(\mathrm{bc}\right)$
will bee as crooked as y^e Parabola at
the vertex $\mathrm{d}$). Divide y^e other leg $\left(\mathrm{be}\right)$
of y^e Squire into any number of pts,
Then get a plate of Br [illeg] |a|sse &c: $\mathrm{lkfd}$ streight & eaven.
And taking one point $\mathrm{d}$ for y^e vertex of it & another
point $\mathrm{c}$ for y^e Squire to move [illeg] n soe y^t $\mathrm{cd}=\mathrm{cb}=\frac{\mathrm{r}}{2}$, &
wearein [illeg] |g| away y^e edge of the plate untill (y^e [illeg] |S|quire
being erected) $\mathrm{ab}=\mathrm{qd}$. the squire touching y^e plate at
$\mathrm{a}$. thus shall y^e edge $\mathrm{adf}$ become Parabolicall. w^th y^e
$\mathrm{Rad:\; ab}$ describe a circle $\mathrm{adg}$ & by that [meanes] it may
bee knowne when $\mathrm{ab}=\mathrm{a}$. \Instead of y^e leg $\mathrm{be}$ a / Demonstraco
\circle may be used/ Supose $\mathrm{aq}=\mathrm{y}$. $\mathrm{cd}=\mathrm{cb}=\frac{\mathrm{r}}{2}$ then [illeg] . Then is [illeg] $\sqrt{\frac{\mathrm{r}\mathrm{r}}{4}}+$ [illeg] $\mathrm{z}\mathrm{z}$ [illeg] $\mathrm{cq}$ [illeg] $\mathrm{ad}=\sqrt{\mathrm{x}\mathrm{x}+\mathrm{y}\mathrm{y}}=\mathrm{ab}$. & $\mathrm{ac}=\sqrt{\frac{\mathrm{r}\mathrm{r}}{4}+\mathrm{x}\mathrm{x}+\mathrm{y}\mathrm{y}}$.
[illeg] |A|nd $\mathrm{cq}=\sqrt{\frac{\mathrm{r}\mathrm{r}}{4}+\mathrm{x}\mathrm{x}}$. & $\mathrm{dq}=\mathrm{x}$. Demonstracon.
$\mathrm{qd}=\mathrm{x}$. $\mathrm{cd}=\frac{\mathrm{r}}{2}=\mathrm{cb}$. $\mathrm{cq}=\frac{\mathrm{r}}{2}-\mathrm{x}$. $\mathrm{aq}=\sqrt{\mathrm{r}\mathrm{x}}=\mathrm{y}$. ${\mathrm{ac}}^2=\frac{\mathrm{r}\mathrm{r}}{4}+\mathrm{x}\mathrm{x}$
${\mathrm{ab}}^2=\frac{\mathrm{r}\mathrm{r}}{4}+\mathrm{x}\mathrm{x}-\frac{\mathrm{r}\mathrm{r}}{4}$ & $\mathrm{ab}=\mathrm{x}$. Q.E.D.

Another description of y^e Parabola y |w| ^e  [sic] y^e
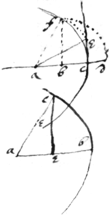
compasses. Make $\mathrm{ab}=\mathrm{bc}=\frac{\mathrm{r}}{4}$. Make $\mathrm{ce}=\mathrm{cd}$
& $\mathrm{ce}⟂\mathrm{bd}$. Make $\mathrm{af}=\mathrm{ae}$, & $\mathrm{bf}=\mathrm{bd}$
then shall $\mathrm{f}$ be a point in y^e Parabola.

Another. [illeg] |M|ake $\mathrm{ab}=\frac{\mathrm{r}+\mathrm{x}}{2}=\mathrm{ac}$. | $\mathrm{eb}=\mathrm{x}⟂\mathrm{ce}$ |
& y^e point $\mathrm{c}$ shall bee in y^e parabola.
This like y^e first by calculation may bee
made use of in other lines.