M^r Mercator lived \above/ 10 or     year [illeg] |s| longer without proceeding further
then to y^e single Quadature [sic] of the Hyperbola. The progress made by M^r
Newton shews that he wanted not Mercators assistance. However, for
avoyding disputes, he supposes ^a 1 that my L Brunker invented & Mercator
demonstrated the series for the Hyperbola three or four \some/ years before they
published it.

The \aforesaid/ treatise of Analysis M^r Newton in his Letter \to M^r Oldenburg/ dated
24 Octob. 1676 mentions in the following manner. Eo ipso tempore &c

When M^r Newton had explained these three Rules & illustrated
then w^th various examples, he layd down the Idea of deducing the
area from the Ordinate by considering the Area as a quantity
g growing or increasing by continual [illeg] motion flux & becoming bigger
or less or in a given accordingly as the \increase or/ flux is swifter or slower
And this flux he measured by the length of the Ordinate supposing
this Ordinate to mo the Abscissa to increase uniformly in proportion
to time. And from the moments of time he calls the gi |a|ves the names
of moments to the parts of the Abscissa & Area generated in moments
of time momentaneus increases or \infinitely [illeg] small/ parts of the Abscissa & Area gene
rated in moments of time. The moment of a line he called a point in
the sense of Cavallerius tho it be not a gemetrical point but an infi
nitely short line & the moment of an Area or superficies he calls |e|d
a line in the sense of Cavallerius tho it be not a Geometrical line
but an infinitely narrow superficies. | The Abscissa he supposes to increase uniformly as the exponent of time | And when he is demonstrating any
Proposition he puts a line drawn into the Abscissa for the exponent of time
& a moment of the Abscissa drawn into y^e Ordinate for the a moment
of the Area. And tells use that And when he considered the Ordinate as the
exponent of time moment of the Area he understan |oo|ds by it the rectangle
under the Geometrical Ordinate & a moment of the Abscissa, as in the
method of Cavallerius; & puts the rectangle under \assumed/ an unit for the ordinate
of a rectangle proportial [sic] to time. [And then adds: Iam qua ratione super-
ficies [curvilinea] ex momento suo perpetim dato, per præcedentes Regulas
elicitur, eadem quælibet alia quantitas ex momento suo sic dato elicietur
And of this he gives example] \ Sit ABD saith he, Curva quævis, et ABH rectangulum cujus latus AH vel BK est unitas. Et / Et [sic] Cogita rectam DBK (saith he)
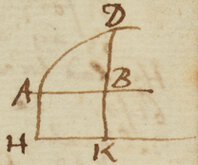
uniformiter ab AH motam areas ABD [curvilineam] & AK
[rectangulam] describere; & quod BK (1) [recta] BK (1) sit
momentum quo [area] ABD gradatim augetur; & AK (x)
& \[recta]/ BD (y) momentum quo ABD [area] AB curilinea] AK [x] ABD
gradatim augetur; et quod ex momenta |o| BD perpetim dato possis, per
præcedentes [tres] Regulas, aream ABD ipso descriptam conferre investigare
sive cum \ [illeg] [ipsius]/ AK (x) momento 1 descripta conferre. Iam qua ratione super
ficies ABD ex momento suo perpetim dato per præcedentes Regulas elicitur
eadem quælibet alia quantitas ex momento suo sic dato elicietur. Exemplo
res fiet clarior. And Then he adds examples of this by finding a series for
the arc of & how \illustrated this w^th examples/ & added his method of Regression from the Area or Arc \or solid/ to
the Abscissa, A |&| shews |e|d how the same method extende |s| d to Mechanical Curves