☞ Note y^t if there happen to bee in any equation either a \fraction or/ surde quantity
or a Mechanichall one, (i:e: w^ch cannot bee Geometrically computed, but is
expressed by y^e [illeg] \area/ or length or gravity or content of some curve line or sollid, &c)
To find in what proportion they \unknowne quantitys/ increase or decrease doe thus. |1| Take two letters
y^e one (as ξ) to signify y^t quantity, y^e other (as χ π) its motion of increase or
decrease: And making an equation betwixt y^t | y^e | letter (ξ) & y^e quantity signifyed
by it, find thereby (by prop 7 if y^e Equation \quantity/ bee Geometricall, or by some other
meanes if it bee mechanicall) y^e valor of y^e other letter (π). |2| Then substi-
tuting y^e letter (ξ) signifying y^t quantity, into its place in y^e maine Equation
esteeme y^t letter (ξ) as an unknowne quantity & performe y^e worke of
seaventh proposition; & into y^e resulting Equation instead of those letters
ξ & π substitute theire valors. And soe you have y^e Equation required.

Example 1. To find p & q y^e motions of x & y whose relation is, $\mathrm{yy}=\mathrm{x}\sqrt{\mathrm{aa}-\mathrm{xx}}$.
first suppose $\mathrm{\xi }=\sqrt{\mathrm{aa}-\mathrm{xx}}$, Or $\mathrm{\xi \xi }+\mathrm{xx}-\mathrm{aa}=0$. & thereby find π y^e motion of ξ, viz:
(by prop 7) $2\mathrm{\pi \xi }+2\mathrm{px}=0$. Or $\frac{-\mathrm{px}}{\mathrm{\xi }}=\mathrm{\pi }=\frac{-\mathrm{px}}{\sqrt{\mathrm{aa}-\mathrm{xx}}}$. Secondly in y^e Equation $\mathrm{yy}=\mathrm{x}\sqrt{\mathrm{aa}-\mathrm{xx}}$,
writing ξ in stead of $\sqrt{\mathrm{aa}-\mathrm{xx}}$, the result is $\mathrm{yy}=\mathrm{x\xi }$, whereby find y^e relation of y^e
motions p, q, & π: viz (by prop 7) $2\mathrm{qy}=\mathrm{p\xi }+\mathrm{x\pi }$. In w^ch Equation instead of ξ
& π writing theire valors, y^e result is, $2\mathrm{qy}=\mathrm{p}\sqrt{\mathrm{aa}-\mathrm{xx}}\frac{-\mathrm{pxx}}{\sqrt{\mathrm{aa}-\mathrm{xx}}}$. w^ch was required \to/.

[w^ch equation multiplyed by $\sqrt{\mathrm{aa}-\mathrm{xx}}$, is $2\mathrm{qy}\sqrt{\mathrm{aa}-\mathrm{xx}}=\mathrm{paa}-2\mathrm{pxx}$. & in stead of
$\sqrt{\mathrm{aa}-\mathrm{xx}}$, writing its valor $\frac{\mathrm{yy}}{\mathrm{x}}$, it is $\frac{2{\mathrm{qy}}^3}{\mathrm{x}}=\mathrm{paa}-2\mathrm{pxx}$. Or $2{\mathrm{qy}}^3=\mathrm{paax}-2\mathrm{pxxx}$. Which [sic]
Which conclusion will also bee found by taking y^e surde quantity out y^e given Equation
for both parts being squared it is ${\mathrm{y}}^4=\mathrm{aaxx}-{\mathrm{x}}^4$. & therefore (by prop 7) $4{\mathrm{py}}^3=2\mathrm{qaax}-4{\mathrm{x}}^3$,
as before.]

☞ Note also y^t it may bee more convenient \(setting all y^e termes on one side of y^e Equation)/ to put [illeg] every fractionall, irrationall
& mechanicall terme, as also y^e summe of y^e rationall termes, equall severally to
some letter: & then to find y^e motions corresponding to each letter of those
letters y^e sume of w^ch motions is y^e Equation required.

Example y^e 2^d. If ${\mathrm{x}}^3-\mathrm{ayy}+\frac{{\mathrm{by}}^3}{\mathrm{a}+\mathrm{y}}-\mathrm{xx}\sqrt{\mathrm{ay}+\mathrm{xx}}=0$ is y^e relation twixt x & y, whose motions
p & q are required. I make ${\mathrm{x}}^3-\mathrm{ayy}=\mathrm{\tau }$; $\frac{{\mathrm{by}}^3}{\mathrm{a}+\mathrm{y}}=\mathrm{\phi }$; & $-\mathrm{xx}\sqrt{\mathrm{ay}+\mathrm{xx}}=\mathrm{\xi }$. & y^e motions of τ, φ, &
ξ being called β, γ, & δ; y^e first Equation [illeg] ${\mathrm{x}}^3-\mathrm{ayy}=\mathrm{\tau }$, gives (by prop 7) $3\mathrm{pxx}-2\mathrm{qay}=\mathrm{\beta }$. y^e
second ${\mathrm{by}}^3=\mathrm{a\phi }+\mathrm{y\phi }$, gives $3\mathrm{qbyy}=\mathrm{a\gamma }+\mathrm{y\gamma }+\mathrm{q\gamma }$; Or $\frac{3\mathrm{qbyy}-\mathrm{q\phi }}{\mathrm{a}+\mathrm{y}}=\mathrm{\gamma }=\frac{3\mathrm{qabyy}+2\mathrm{qb}{\mathrm{y}}^3}{\mathrm{aa}+2\mathrm{ay}+\mathrm{yy}}$.
& y^e Third $\mathrm{ay}{\mathrm{x}}^4+{\mathrm{x}}^6=\mathrm{\xi \xi }$, gives, ${\mathrm{qax}}^4+4{\mathrm{payx}}^3+6{\mathrm{px}}^5=2\mathrm{\delta \xi }$; Or $\frac{-\mathrm{qaxx}-4\mathrm{payx}-6{\mathrm{px}}^3}{2\sqrt{\mathrm{ay}+\mathrm{xx}}}=\mathrm{\delta }$.
Lastly $\mathrm{\beta }+\mathrm{\gamma }+\mathrm{\delta }=3\mathrm{pxx}-2\mathrm{qay}\frac{+3\mathrm{qabyy}+2{\mathrm{qby}}^3}{\mathrm{aa}+2\mathrm{ay}+\mathrm{yy}}\frac{-\mathrm{qaxx}-4\mathrm{payx}-6{\mathrm{px}}^3}{2\sqrt{\mathrm{ay}+\mathrm{xx}}}=0$, is y^e Equation sought.

Example 3^d. If $\mathrm{x}=\mathrm{ab}\perp \mathrm{bc}=\sqrt{\mathrm{ax}-\mathrm{xx}}$. be=y. & y^e superficies abc=z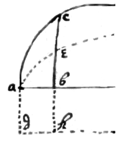
suppose y^t ax+xz−y³ $\mathrm{zz}+\mathrm{axz}-{\mathrm{y}}^4=0$, is y^e relation twixt x, y & z,
whose motions are p, q, & r: & y^t p & q are desired. The Equation
$\mathrm{zz}+\mathrm{axz}-{\mathrm{y}}^4=0$ gives (by prop 7), $2\mathrm{rz}+\mathrm{rax}+\mathrm{paz}-4{\mathrm{qy}}^3=0$. Now drawing
dh∥ab⊥ad=1−bh. I consider y^e superficies abhd=ab×bh=x×1=x, &
abd=z doe increase in y^e proportion of bh to bc: yt is, 1∶$\sqrt{\mathrm{ax}-\mathrm{xx}}$∷p∶r.
Or $\mathrm{r}=\mathrm{p}\sqrt{\mathrm{ax}-\mathrm{xx}}$. Which valor of r being substituted into y^e Equation
$2\mathrm{rz}+\mathrm{rax}+\mathrm{paz}-4{\mathrm{qy}}^3=0$, gives $\overline{2\mathrm{pz}+\mathrm{pax}}\times \sqrt{\mathrm{ax}-\mathrm{xx}}+\mathrm{paz}-4{\mathrm{qy}}^3=0$. w^ch was required.

How to proceede in other cases (as when there are cube rootes, surde denominators, rootes
within rootes (as $\sqrt{\mathrm{ax}+\sqrt{\mathrm{aa}-\mathrm{xx}}}$ &c: in the equation) may bee easily bee deduced from what
[ha]th bee[n] already said.