Prob 15. To find y^e Gravity of any given plaine in respect of any given axis, given in position
when it may bee done.

Resol: Suppose ek to bee y^e Axis of Gravity, acb the given plaine,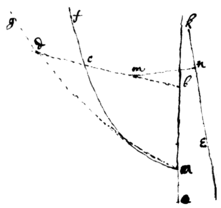
cb=y, & db=z to bee ordinatly applyed at any angles to ab=x. Bisect
cb at m & draw mn⊥ek. Now, since [cb×mn] is y^e gravity of y^e
line [cb], (by lem 1 & 2); if I make cb×mn=db=z, every line db shall
designe y^e Gravity of its correspondent line cb, y^t is, y^e superficies adb
shall designe y^e Gravity of y^e superficies acb. Soe y^t finding y^e quantity
of y^t superficies adb (by prob 7) I find y^e gravity of y^e sup [illeg]e |er|ficies acb.

Example 1 If ac is a Parabola; soe y^t , ab[illeg] bc=[4], & z=d[a]∥k
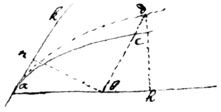
parallelTo;ak=axis rx=yy, & y^e axis ak is ∥ dcb. &, [illeg]
nb⊥ak, & y^t , ab∶nb∷d∶e. Then is bc×nb=y×$\frac{\mathrm{e}\times \mathrm{ab}}{\mathrm{d}}=\frac{\mathrm{ex}}{\mathrm{d}}\sqrt{\mathrm{rx}}=\mathrm{z}$.
Or eerx³=ddzz, is y^e nature of y^e curve line ad. whose
area (were [illeg] abd a right angle would be $\frac{2\mathrm{e}}{5\mathrm{d}}{\mathrm{x}}^{\frac{5}{2}}{\mathrm{y}}^{\frac{1}{2}}=\frac{2\mathrm{e}}{5\mathrm{d}}\sqrt{\mathrm{r}{\mathrm{x}}^5}$ but now it) is $\frac{2\mathrm{ee}}{5\mathrm{dd}}\sqrt{\mathrm{r}{\mathrm{x}}^5}$, (by
prob 7) w^ch is y^e weight of y^e area acb in respect of y^e axis ak.

Examp: 2 If ac is a Circle

Prob 16. To find y^e Axes of Gravity i |o|f any Plaines

Resol. Find y^e quantity of y^e Plaine (by Prob 7) \ w^ch call A/ & y^e quantity of its gravity in respect
of any axis (by prob 15) w^ch call B [illeg] . & parallell to y^t axis draw a line whose distance
from it shall bee [illeg] $\frac{\mathrm{A}}{\mathrm{B}}$. That line shall bee an Axis of Gravity of y^e given plain

Or If you y cannot find y^e quantity of the plane: Then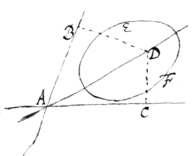
find its gravitys in respect of two divers axes (AB & AC) w^ch gravitys
call B[illeg] & C & D. & through |(A)| y^e intersection of those axes draw
a line AD w^th this condition y^t y^e distances (DB & DC) of any one
of its points (D) from the said axes (AB & AC), bee in such proportion as \to/ the gravitys
of the plane. That line (AD) shall bee an axis of gravity of y^e said plane EF.